Trapping Rain Water II

Given n x m non-negative integers representing an elevation map 2d where the area of each cell is 1 x 1, compute how much water it is able to trap after raining.

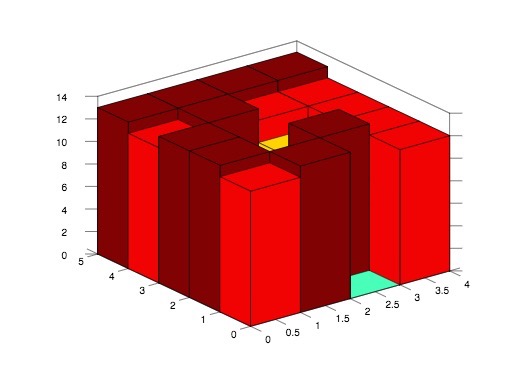
Example:

Given 5*4 matrix

[12,13,0,12]
[13,4,13,12]
[13,8,10,12]
[12,13,12,12]
[13,13,13,13]

return 14.

Solution:

This problem requires a combination of PriorityQueue and Depth First Search. We use the outermost element as the boundary, because the water can only be trapped inside some boundaries. Since we want to start with the lowest boundary value, we have to add all the boundary values into a min PriorityQueue.

When we start with the lowest boundary value, we could explore its unvisited neighbors. If a neighbor is less than lowest boundary value, we use the difference as the amount of water trapped on that point and add this neighbor into the queue with lowest boundary value. If a neighbor is greater than lowest boundary value, we simply add it into the queue.

We repeat above process until the queue is empty.

Code:

public class Solution {
    /**
     * @param heights: a matrix of integers
     * @return: an integer
     */
    final static int[] dr = {1, -1, 0, 0};
    final static int[] dc = {0, 0, 1, -1};
    public int trapRainWater(int[][] heights) {
        if (heights == null || heights.length == 0 || heights[0].length == 0) {
            return 0;
        }
        int res = 0;
        int m = heights.length;
        int n = heights[0].length;

        Queue<DataNode> q = new PriorityQueue<>(m * n);
        boolean[][] visited = new boolean[m][n];
        for (int i = 0; i < m; i++) {
            visit(i, 0, 0, heights, visited, q);
            visit(i, n - 1, 0, heights, visited, q);
        }
        for (int j = 0; j < n; j++) {
            visit(0, j, 0, heights, visited, q);
            visit(m - 1, j, 0, heights, visited, q);
        }
        while (!q.isEmpty()) {
            DataNode node = q.poll();
            int r = node.r;
            int c = node.c;
            int h = node.h;
            for (int i = 0; i < 4; i++)  {
                res += visit(r + dr[i], c + dc[i], h, heights, visited, q);
            }
        }
        return res;
    }

    private int visit(int i, int j, int fromHeight, int[][] heights, 
                            boolean[][] visited, Queue<DataNode> q) {
        if (i < 0 || i >= heights.length || j < 0 || j >= heights[i].length) {
            return 0;
        }
        if (visited[i][j]) {
            return 0;
        }
        q.offer(new DataNode(i, j, Math.max(fromHeight, heights[i][j])));
        visited[i][j] = true;
        return Math.max(0, fromHeight - heights[i][j]);
    }

    class DataNode implements Comparable<DataNode> {
        int r;
        int c;
        int h;
        public DataNode(int row, int col, int height) {
            r = row;
            c = col;
            h = height;
        }
        @Override public int compareTo(DataNode that) {
            return this.h - that.h;
        }
    }
};