K Closest Numbers In Sorted Array

Given a target number, a non-negative integer k and an integer array A sorted in ascending order, find the k closest numbers to target in A, sorted in ascending order by the difference between the number and target. Otherwise, sorted in ascending order by number if the difference is same.

Example:

Given A = [1, 2, 3], target = 2 and k = 3, return [2, 1, 3].

Given A = [1, 4, 6, 8], target = 3 and k = 3, return [4, 1, 6].

Challenge:

O(logn + k) time complexity.

Solution:

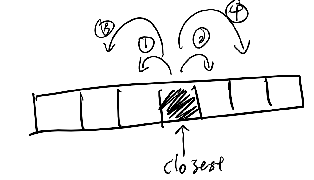
1. Find the closest number in the input array.
2. Use two pointers left and right to search the neighbor of the closest number.

Code:

public int[] kClosestNumbers(int[] A, int target, int k) {
    if (A == null || A.length == 0) {
        return new int[]{};
    }
    int closest = findClosest(A, target);
    //define left = closest - 1, will put the smaller closest in the front
    int left = closest - 1;
    int right = closest;
    int[] result = new int[k];
    for (int i = 0; i < k; i++) {
        if (left < 0) {
            result[i] = A[right++];
        } else if (right >= A.length) {
            result[i] = A[left--];
        } else {
            if (Math.abs(A[left] - target) <= Math.abs(A[right] - target)) {
                result[i] = A[left--];
            } else {
                result[i] = A[right++];
            }
        }
    }
    return result;
}
private int findClosest(int[] A, int target) {
    int start = 0;
    int end = A.length - 1;
    while (start + 1 < end) {
        int mid = start + (end - start) / 2;
        if (target > A[mid]) {
            start = mid;
        } else if (target < A[mid]) {
            end = mid;
        } else {
            return mid;
        }
    }
    //since we define left as closest - 1, the output of this function should be the larger closest.
    if (A[start] >= target) {
        return start;
    }
    if (A[end] >= target) {
        return end;
    }
    return A.length - 1;
}