Sliding Window Matrix Maximum

Given an array of n * m matrix, and a moving matrix window (size k * k), move the window from top left to botton right at each iteration, find the maximum number inside the window at each moving.

Return 0 if the answer does not exist.

Example:

For matrix

[
  [1, 5, 3],
  [3, 2, 1],
  [4, 1, 9],
]

The moving window size k = 2.

[
  [1, 5, 3],
  [3, |2, 1|],
  [4, |1, 9|],
]

return sum to 13.

Solution:

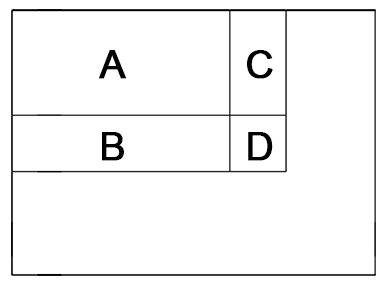
Assume D is a size k by k kernel matrix and its right bottom index is (i, j), we could easily get D by ABCD - AC - AB + A, where

• A is the sum from (0, 0) to (i - k, j - k),
• AC is the sum from (0, 0) to (i - k, j),
• AB is the sum from (0, 0) to (i, j - k),
• ABCD is the sum from (0, 0) to (i, j)

Therefore, if we could calculate all the sums for any point in O(n^2), this problem is solved in O(n^2).

When we conduct this concept again for computing sum from (0, 0) to (i, j), we will have ABCD = AC + AB + D - A, now, this time the D is a size 1 by 1 kernel which means D is an element of matrix.

$$sum[i][j] = sum[i - 1][j] + sum[i][j - 1] + matrix[i - 1][j - 1] - sum[i - 1][j - 1]$$

Note: our sum have one extra column and row for initialization.

Code:

public class Solution {
    /**
     * @param matrix an integer array of n * m matrix
     * @param k an integer
     * @return the maximum number
     */
    public int maxSlidingMatrix(int[][] matrix, int k) {
        if (matrix == null) {
            return 0;
        }
        int m = matrix.length;
        if (m == 0 || m < k) {
            return 0;
        }
        int n = matrix[0].length;
        if (n == 0 || n < k) {
            return 0;
        }
        int[][] sum = new int[m + 1][n + 1];

        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                sum[i][j] = matrix[i - 1][j - 1] + sum[i - 1][j] + sum[i][j - 1]
                                - sum[i - 1][j - 1];
            }
        }
        int max = Integer.MIN_VALUE;
        for (int i = k; i <= m; i++) {
            for (int j = k; j <= n; j++) {
                int windowSum = sum[i][j] - sum[i - k][j] - sum[i][j - k] 
                                + sum[i - k][j - k];
                max = Math.max(max, windowSum);
            }
        }
        return max;
    }
}