Find Peak Element

There is an integer array which has the following features:

• The numbers in adjacent positions are different.
• A[0] < A[1] && A[A.length - 2] > A[A.length - 1].

We define a position P is a peek if:

• A[P] > A[P-1] && A[P] > A[P+1]

Find a peak element in this array. Return the index of the peak.

The array may contains multiple peeks, find any of them.

Example:

Given [1, 2, 1, 3, 4, 5, 7, 6]

Return index 1 (which is number 2) or 6 (which is number 7).

Solution:

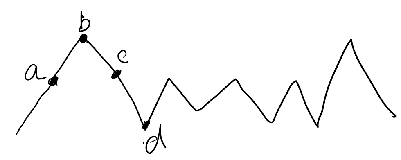
As shown in above, for any mid element in this array, there are only four scenarios:

1. Uphill (point a): A[i - 1] < A[i] && A[i] < A[i + 1], we could set mid to start
2. Peak (point b): A[i - 1] < A[i] && A[i] > A[i + 1], return mid
3. Downhill (point c): A[i - 1] > A[i] && A[i] > A[i - 1], we could set mid to end
4. Bottom (point d): A[i - 1] > A[i] && A[i] < A[i + 1], we could set mid to start or end

To simplify it, we set mid to start when A[i] > A[i - 1], and set mid to end for all other cases.

Code:

public int findPeak(int[] A) {
    if (A == null || A.length == 0) {
        return -1;
    }
    int start = 1;
    int end = A.length - 1;
    while (start + 1 < end) {
        int mid = start + (end - start) / 2;
        if (A[mid] > A[mid - 1]) {
            start = mid;
        } else {
            end = mid;
        }
    }
    if (A[start] > A[end]) {
        return start;
    } else {
        return end;
    }
}