Maximal Square

Given a 2D binary matrix filled with 0's and 1's, find the largest square containing all 1's and return its area.

Example:

For example, given the following matrix:

1 0 1 0 0
1 0 1 1 1
1 1 1 1 1
1 0 0 1 0

Return 4.

Solution:

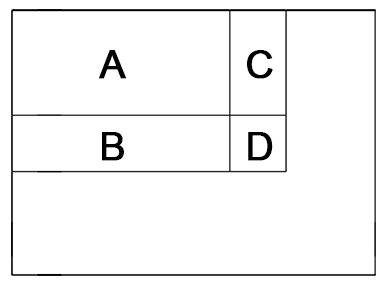
Similar to Sliding Window Matrix Maximum. The largest square is defined by the maximum length of that square. Therefore, we could create a matrix to store the maximum length of continue 1s. The maximum length of continue 1s in cell D (f[i][j)] could be defined by the min of maximum length in A, B and C plus 1, when matrix[i-1][j-1] == 1. Otherwise, f[i][j] = 0.

Code:

public class Solution {
    /**
     * @param matrix: a matrix of 0 and 1
     * @return: an integer
     */
    public int maxSquare(int[][] matrix) {
        if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
            return 0;
        }
        int m = matrix.length;
        int n = matrix[0].length;
        int[][] f = new int[2][n + 1];
        int res = 0;
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                if (matrix[i - 1][j - 1] != 0) {
                    f[i % 2][j] = Math.min(f[(i - 1) % 2][j], 
                                    Math.min(f[i % 2][j - 1], f[(i - 1) % 2][j - 1])) + 1;
                } else {
                    f[i % 2][j] = 0;
                }
                if (f[i % 2][j] > res) {
                    res = f[i % 2][j];
                }
            }
        }
        return res * res;
    }
}