Largest Rectangle in Histogram

Given n non-negative integers representing the histogram's bar height where the width of each bar is 1, find the area of largest rectangle in the histogram.

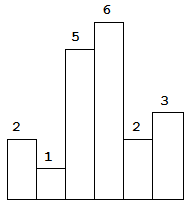
Above is a histogram where width of each bar is 1, given height = [2,1,5,6,2,3].

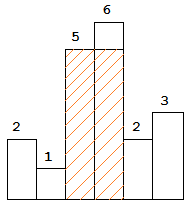
The largest rectangle is shown in the shaded area, which has area = 10 unit.

Example:

Given height = [2,1,5,6,2,3],

return 10.

Solution:

The naive solution for this problem is using two nested for loops. Outer loop iterates through each possible starting element and inner loop is used for ending element. The max areas between the starting element and ending element will be the result. O(n^2) with O(1) space.

Increasing stack is a stack which only contains number in increasing order. If new element is less than some elements in the stack, the increasing stack has to pop out all those elements out before pushing the new element in. By using this increasing stack, this problem could be solved in O(n) with O(n) space.

We push indices of elements from the given height to increasing stack. Since the stack is increasing, the largest element is siting at the end of the stack. When a new element comes in, if this element is greater than the existing largest element, we push the index of this new element into our stack. Otherwise, the index of the largest element needs to be popped out and calculate the area between that index to current element's index. We repeat this process until the largest area is found.

Code:

public class Solution {
    public int largestRectangleArea(int[] height) {
        if (height == null || height.length == 0) {
            return 0;
        }
        Stack<Integer> stack = new Stack<>();
        int maxArea = Integer.MIN_VALUE;
        for (int i = 0; i <= height.length; i++) {
            int curt = -1;
            if (i < height.length) {
                curt = height[i];
            }
            while (!stack.empty() && curt < height[stack.peek()]) {
                int h = height[stack.pop()];
                //i is the number of item from the beginning to now, when stack is empty
                int w = i; 
                //w is current (right) substract (left) take away one, when stack is not empty 
                if (!stack.empty()) {
                    w = i - stack.peek() - 1;
                }
                maxArea = Math.max(maxArea, h * w);
            }
            stack.push(i);
        }
        return maxArea;
    }
}